


Establishing a consistent normal orientation for point clouds is a notoriously difficult problem in geometry processing, requiring attention to both local and global shape characteristics. The normal direction of a point is a function of the local surface neighborhood; yet, point clouds do not disclose the full underlying surface structure. Even assuming known geodesic proximity, calculating a consistent normal orientation requires the global context. In this work, we introduce a novel approach for establishing a globally consistent normal orientation for point clouds. Our solution separates the local and global components into two different sub-problems. In the local phase, we train a neural network to learn a coherent normal direction per patch (i.e., consistently oriented normals within a single patch). In the global phase, we propagate the orientation across all coherent patches using a dipole propagation. Our dipole propagation decides to orient each patch using the electric field defined by all previously orientated patches. This gives rise to a global propagation that is stable, as well as being robust to nearby surfaces, holes, sharp features and noise.
Locally, defining what is inside or the outside of the surface ((i.e., which direction the *surface* normal points)), is not well defined:
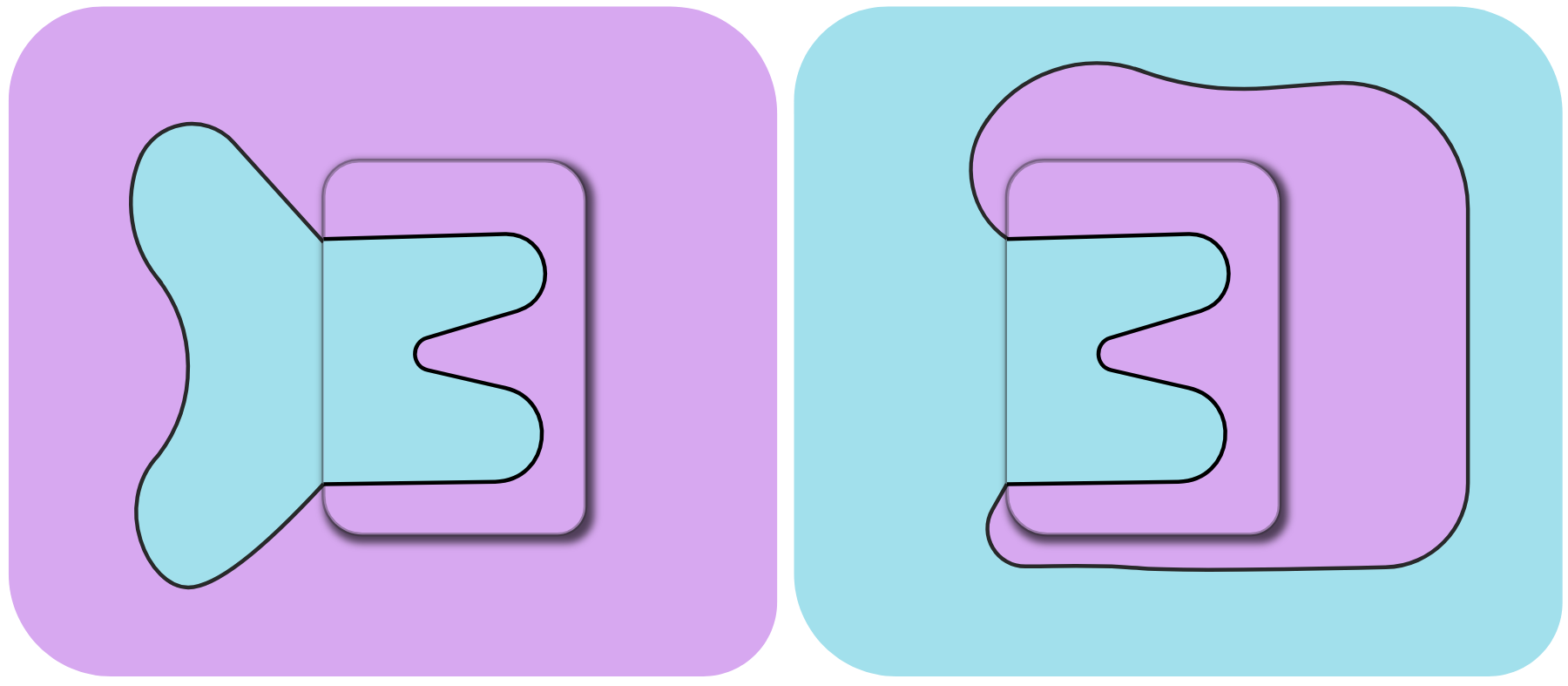
The orientation of the surface in the indicated square, can not be determined without global context of the rest of the shape. To alleviate this problem, we divide the orientation problem into two steps: Local and Global.
We start by orienting each local patch coherently: meaning that all normals in the patch should point either inside or outside the shape. Locally, patches can be very complicated and non-convex, and constructing a hand crafted technique can be especially challenging. Instead, we learn the correct orientation using a neural network, trained on ground truth point clouds sampled from oriented meshes.
Initially, the points are oriented according to a reference point (yellow) placed at the center mass of the patch.
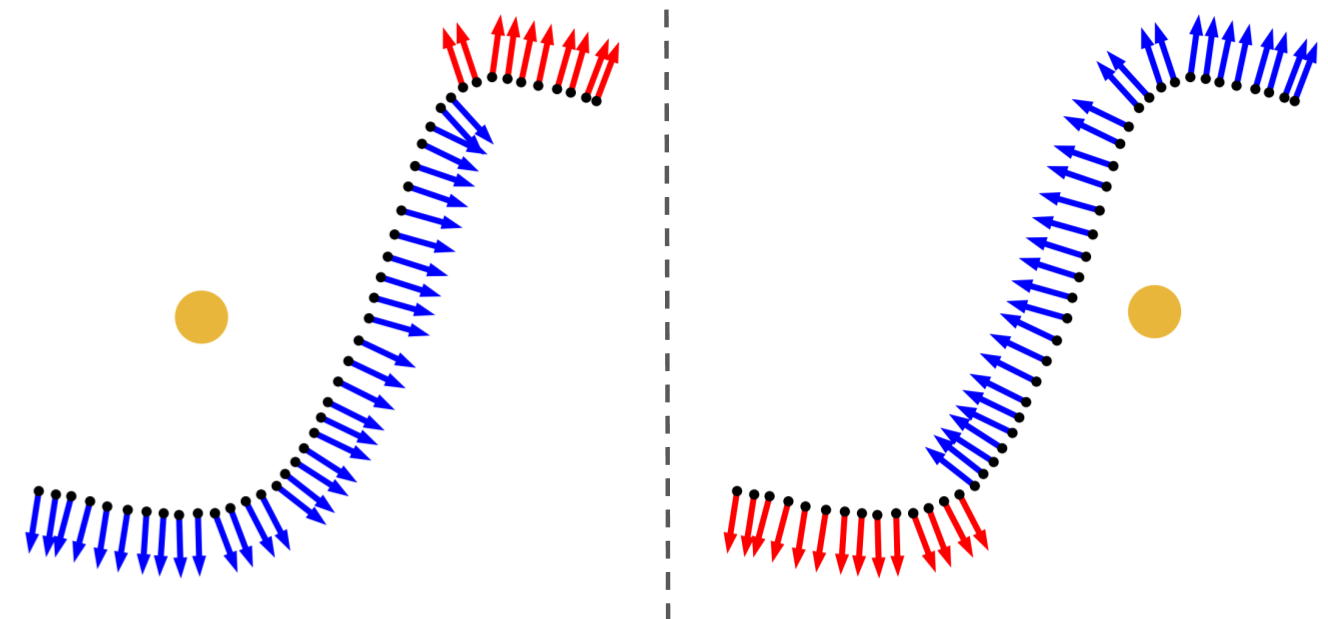
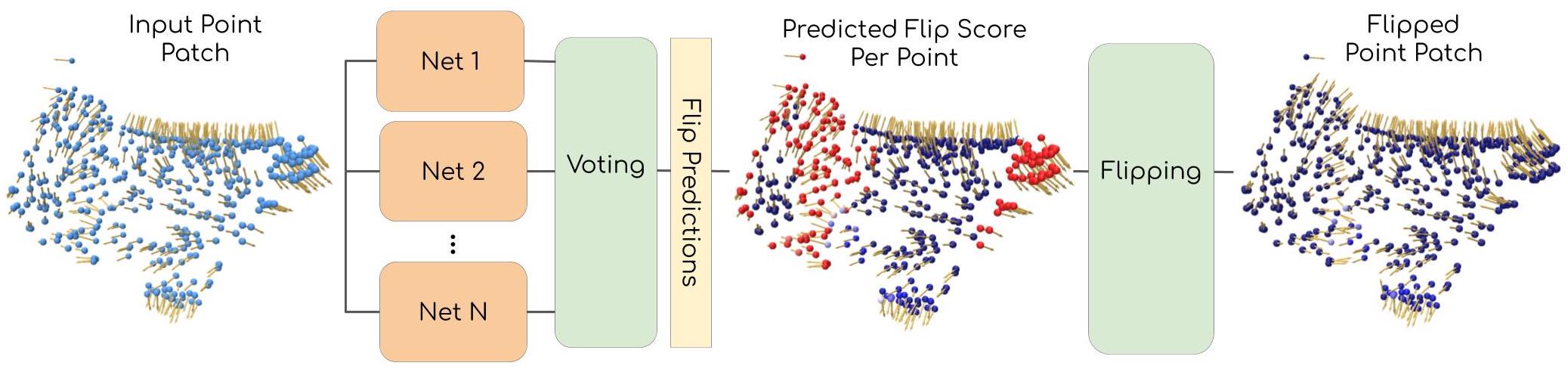
Then, an ensemble of networks decides which points ought to be corrected. Our network is trained to classify the incoherent point normals (in red). After we flip the incoherent point normals, we obtain a coherently oriented patch.
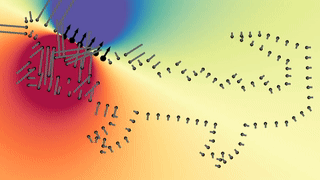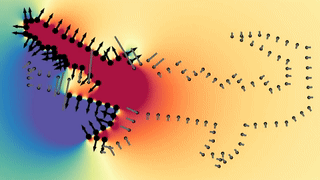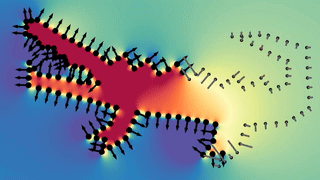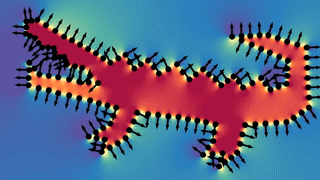
After a collection of coherent patches is constructed, we use a robust and stable dipole propagation technique to align the local patches Globally.
Starting from the flattest patch, a dipole field from each point is iteratively constructed and used to determine the orientation for the rest of the patches. At each step of the algorithm, the patch that has the strongest interaction with the field is selected, and flipped (if needed) to align with the field according to the majority of its points. The field is constructed globally, meaning that all previously oriented patches contribute to the total dipole field, giving global context at each step of the propagation. In addition, the network-predicted confidence scores are used as the dipole magnitude of each point, to prevent accumulative propagation error from uncertain points.

This however does not requires a long time to compute, because a closed solution for the field at each point is available. Also, because the dipole field arise from a solution to the Poisson equation which is linear, the contribution of patches is simply summed up to compute the total field. Allowing to only compute the delta contributions of each newly oriented patch in the iterative propagation process.
We thank Shihao Wu for his helpful suggestions,
and are grateful for rendering help from Tamir Lousky.
This work is supported by the European research council (ERC-StG 757497 PI Giryes),
and the Israel Science Foundation (grants no. 2366/16 and 2492/20).
This work was supported in part through the NYU IT High Performance Computing resources,
services, and staff expertise. This work was partially supported by the NSF CAREER award 1652515,
the NSF grants IIS-1320635, DMS-1436591, DMS-1821334, OAC-1835712, OIA-1937043, CHS-1908767, CHS-1901091,
a gift from Adobe Research, a gift from nTopology, and a gift from Advanced Micro Devices, Inc.