Abstract

We introduce a novel technique for neural point cloud consolidation which learns from only the input point cloud. Unlike other point upsampling methods which analyze shapes via local patches, in this work, we learn from global subsets. We repeatedly self-sample the input point cloud with global subsets that are used to train a deep neural network. Specifically, we define source and target subsets according to the desired consolidation criteria (e.g., generating sharp points or points in sparse regions). The network learns a mapping from source to target subsets, and implicitly learns to consolidate the point cloud. During inference, the network is fed with random subsets of points from the input, which it displaces to synthesize a consolidated point set. We leverage the inductive bias of neural networks to eliminate noise and outliers, a notoriously difficult problem in point cloud consolidation. The shared weights of the network are optimized over the entire shape, learning non-local statistics and exploiting the recurrence of local-scale geometries. Specifically, the network encodes the distribution of the underlying shape surface within a fixed set of local kernels, which results in the best explanation of the underlying shape surface. We demonstrate the ability to consolidate point sets from a variety of shapes, while eliminating outliers and noise.

Self-Sampling Overview

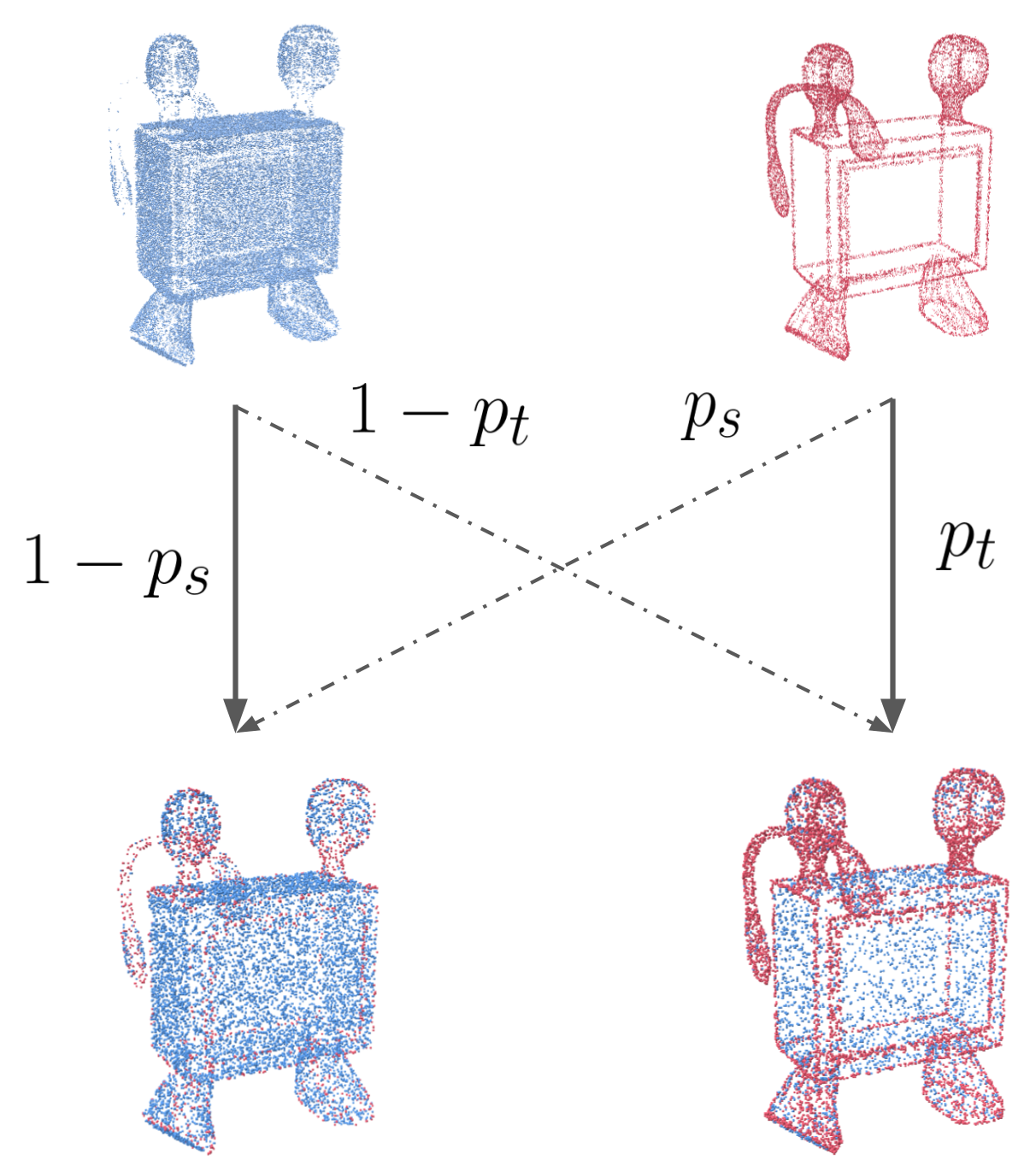
We train a network to generate a consolidated set of points using the self-supervision present within a single input point cloud. We define source (blue) and target (red) subsets according to the desired consolidation criterion (e.g., generating sharp points or points in sparse regions).

We repeatedly self-sample the input point cloud with global subsets which are used to train a deep neural network. The subsets are balanced according to the consolidation criterion, for example sharpness in the example below.

The network is trained on disjoint pairs of source and target subsets, and implicitly learns to consolidate the point cloud by generating offsets which are added to the input source points such that they resemble a target subset (i.e., predicted target subset).

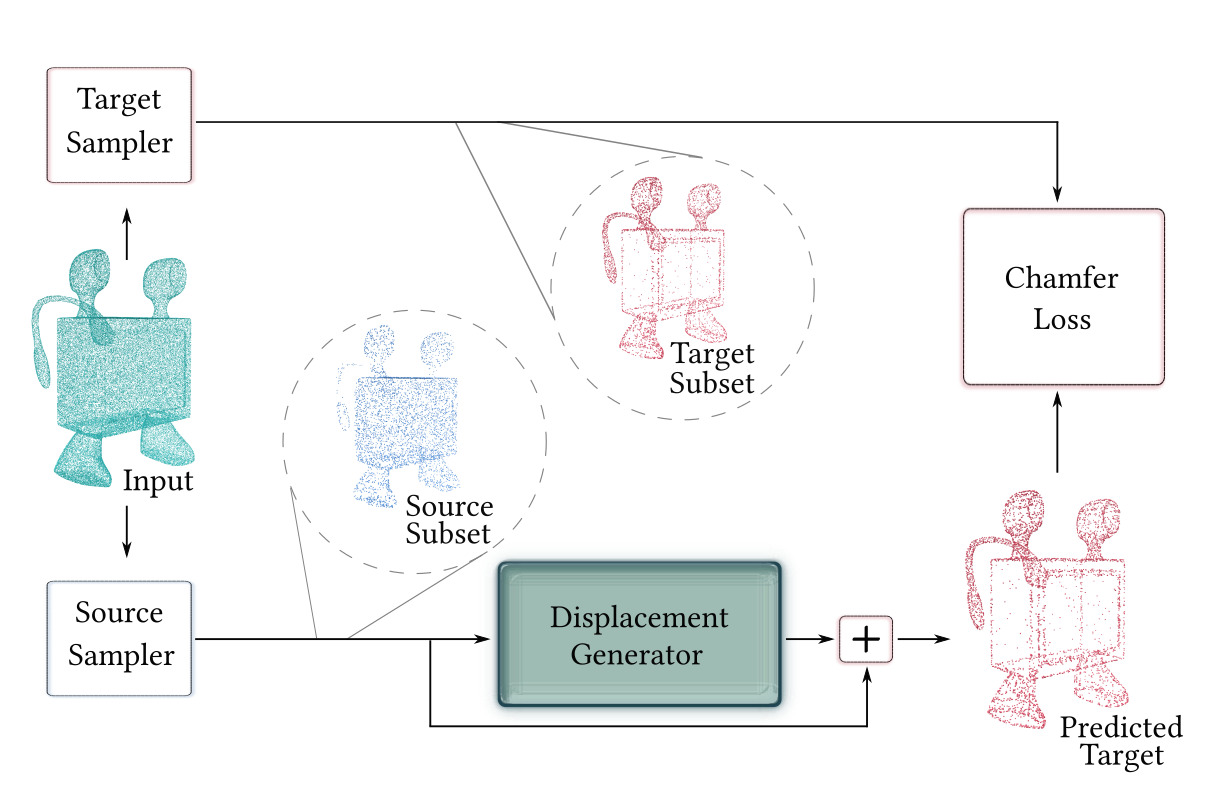
During inference, the network is fed with random subsets of points from the input, which it displaces to synthesize a consolidated point set. This process is repeated to obtain an arbitrarily large set of consolidated points with an emphasis on the consolidation criterion (\emph{e.g.,} sharp feature points or points in sparsely sampled regions).

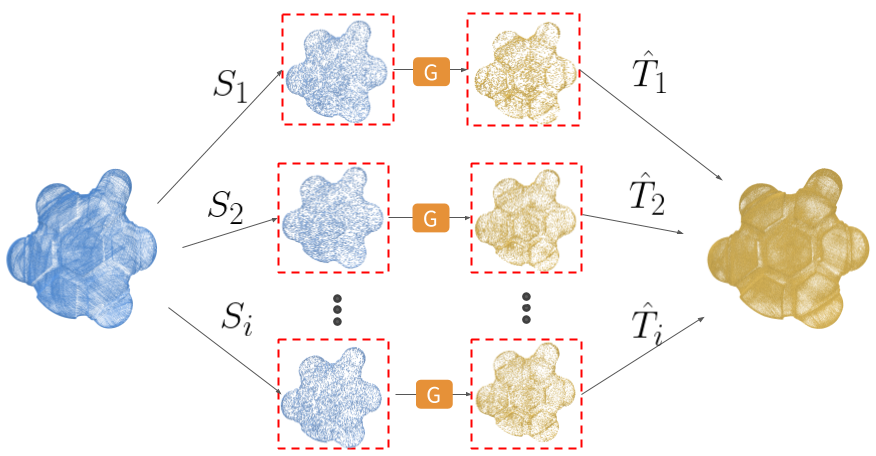
The network is able to generalize and express novelty in the generation of new points at inference time. The diversity in novel sharp feature generation can be seen in the figure below. Given an input point(red) and random subsets from the input point cloud (entire point cloud in blue), our network generates different displacements which are added to the input point to generate a variety of different output points (yellow). Novel points on the surface are conditioned on the selected input subset, and thus can be different at each forward pass.

Results

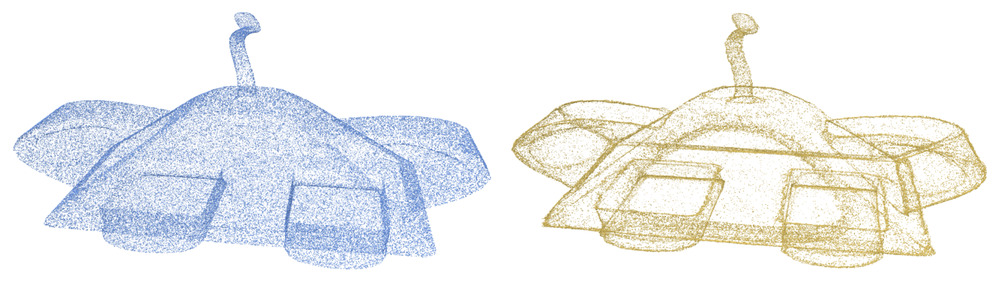
Edge consolidation result of an alien shape with sharp edges.

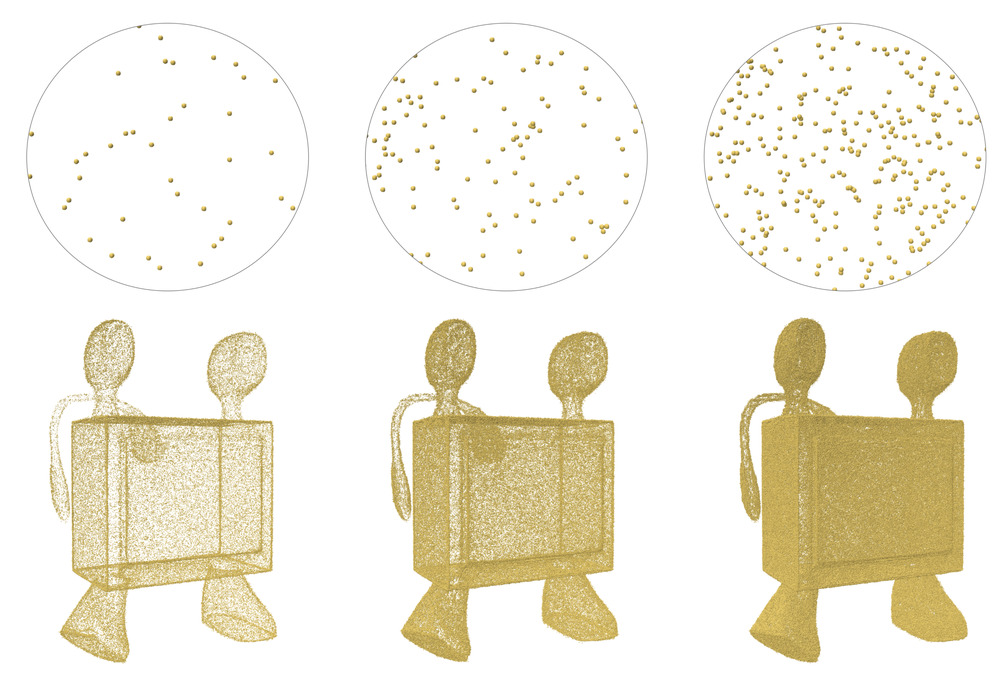
As the number of forward passes increases at inference, the higher the verity of the output is.

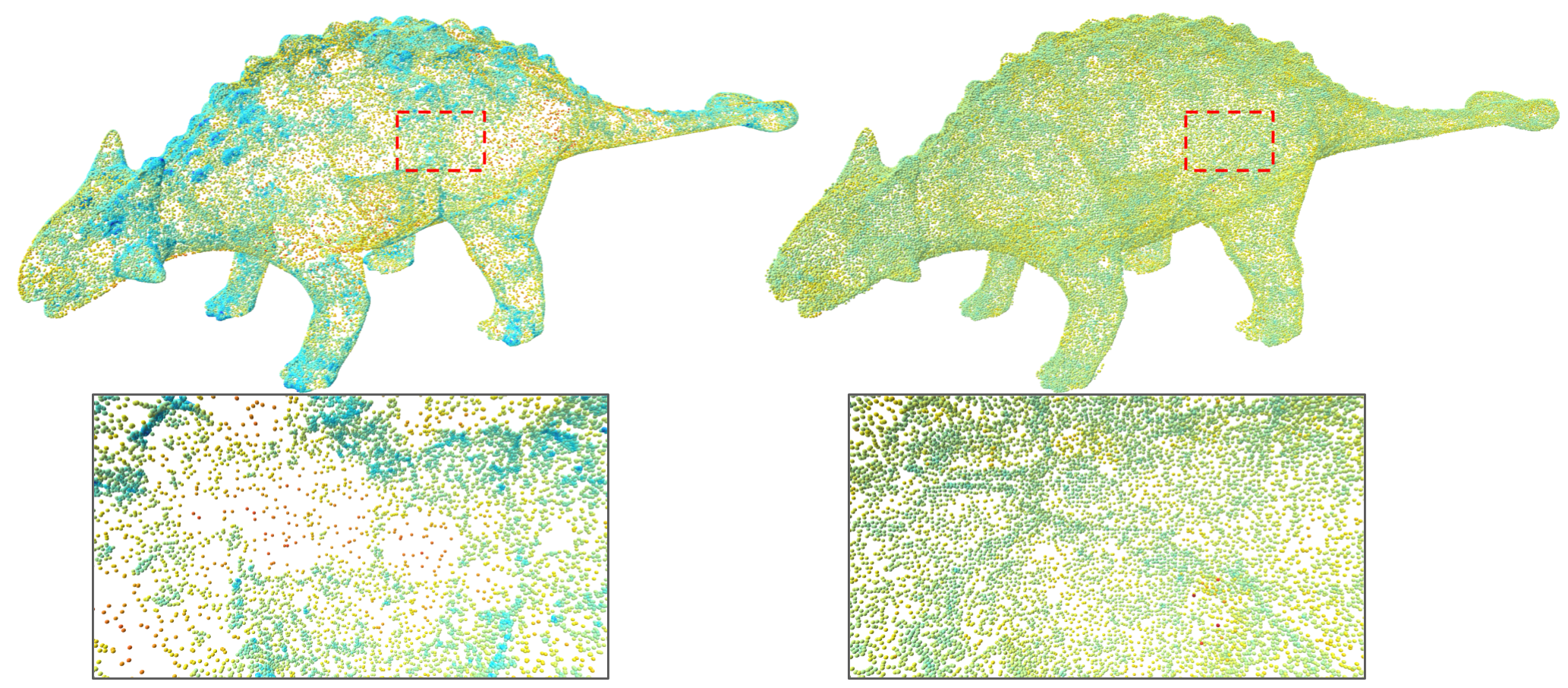
Increasing the density of points in sparse regions leads to a better post process mesh reconstruction.

Left is the real scanned input, middle is EC-Net, and right is ours. A sparsely sampled edges is recovered by our method.

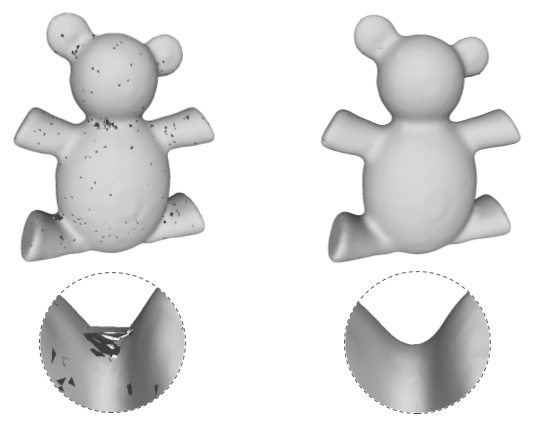
When running our method with random subsampling we achieve denoising, as the network is not able to overfit the noise.

Citation

        @article{metzer2020self,
        author = {Metzer, Gal and Hanocka, Rana and Giryes, Raja and Cohen-Or, Daniel},
        title = {Self-Sampling for Neural Point Cloud Consolidation},
        year = {2021},
        issue_date = {October 2021},
        publisher = {Association for Computing Machinery},
        address = {New York, NY, USA},
        volume = {40},
        number = {5},
        issn = {0730-0301},
        url = {https://doi.org/10.1145/3470645},
        doi = {10.1145/3470645},
        }
        

Acknowledgements

We thank Shihao Wu for his helpful suggestions, and Xianzhi Li for providing data for comparisons.
We also thank Guy Yoffe for providing real point cloud scans.
This work is supported by the European research council (ERC-StG 757497 PI Giryes), and the Israel Science Foundation (grants no. 2366/16 and 2492/20).